1.5.8 Edge Coloring
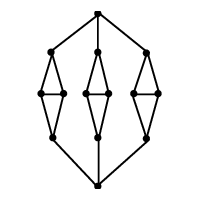
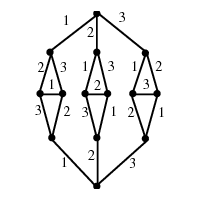
INPUT OUTPUT
Input Description:
A graph G=(V,E).
Problem:
What is the smallest set of colors needed to color the edges
of E such that no two edges with the same color share a vertex
in common?
Excerpt from
The Algorithm Design Manual:
The edge coloring of graphs arises in a variety of scheduling applications,
typically associated with minimizing the number of noninterfering rounds
needed to complete a given set of tasks.
For example, consider a situation where we need to schedule a given
set of two-person interviews, where each interview
takes one hour.
All meetings could be scheduled to occur at distinct times to avoid conflicts,
but it is less wasteful to schedule nonconflicting
events simultaneously.
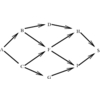
We can construct a graph whose vertices are the people and whose edges
represent the pairs of people who want to meet.
An edge coloring of this graph defines the schedule.
The color classes represent the different time periods in the schedule,
with all meetings of the same color happening simultaneously.
The National Football League solves such an edge coloring problem each
season to make up its schedule.
Each team's opponents are determined by the records of the previous season.
Assigning the opponents to weeks of the season
is the edge-coloring problem, presumably
complicated by the constraints of spacing out rematches and
making sure that there is a good game every Monday night.
The minimum number of colors needed to edge color a graph is
called by some its edge-chromatic number
and others its chromatic index.
To gain insight into edge coloring, note that a graph consisting
of an even-length cycle can be edge-colored
with 2 colors, while odd-length cycles have an edge-chromatic number of 3.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com




 Cliques, Coloring, and Satisfiability: Second Dimacs Implementation Challenge
Cliques, Coloring, and Satisfiability: Second Dimacs Implementation Challenge Graph Coloring Problems
Graph Coloring Problems Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica