Optimal Transportation and Explainable AI
Optimal transportation finds the most economical way to transform one probability measure to the other. Optimal transportation theory
is the intersection among various fields, including probability and statistics, convex differential geometry, fluid dynamics and Monge-Ampere
partial differential equation and so on.
Statistical learning aims at learning probability distributions defined on low dimensional data manifolds embedded in
high dimensional ambient spaces. Therefore the central tasks include learning the manifold structure and the probability distrubitions.
The second task can be accomplished using optimal transportation.
Explainable AI The fundamental principle for deep learning is to perform optimization in the space consisting all probability measures (the Wasserstein space).
Optimal transportation theory assigns a natural Riemannian metric to the Wasserstein space, such that the variational optimization can be
carried out using the covariant calulus. Hence optimal transportation has been broadly applied in deep learning, such as
generative models.
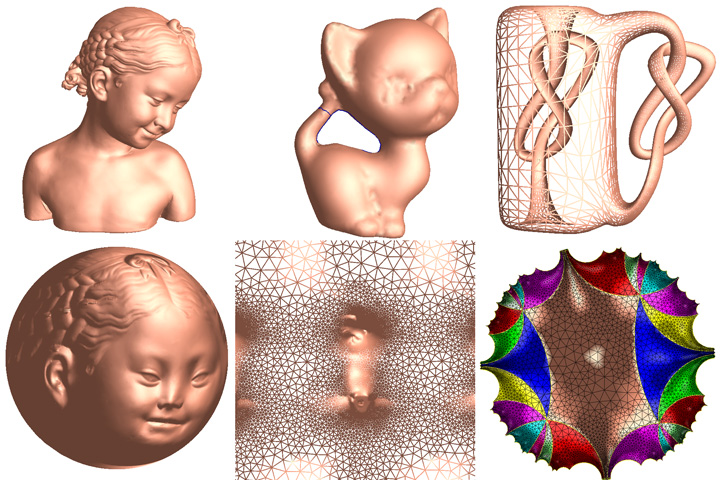
Geometric Variational Algorithm The optimal transportation map is the gradient map of the Brenier potential. Fundamentally, the Brenier theorem in optimal transportation is equivalent to the Alexandrov theorem
in convex geometry, both of them are governed by the Monge-Ampere equation. The Brenier potential (Alexandrov polyhedron) can be computed
by optimizing the Monge transportation cost, or equivalently the volume, using geometric variational algorithm.
Spherical Optimal Transportation Algorithm The spherical optimal transportation map can be solved using the geometric variational
approach as well. The spherical OT map algorithm can be applied to solve the Minkowski problem, which determines the shape from the Gaussian curvature,
and the otpical design problems. The spherical optimal transportation algorithm is based on convex optimization.

|
Explainable AI Optimal transportation lays down the theoretic foundation of deep learning, it can be applied
to explain fundamental problems in deep learning, such as mode collapse. Depending on the supports of the probability measures, the optimal transportation maps may have singuarlities, where the
map is discontinous. In general, deep neural nets can only represent continuous maps. This cause the mode collapsing issue in deep learning.
Therefore, by considering the regularity issue of the optimal transportation maps, we can design generative models to eliminate mode collapse, such as
geometric GAN model.
3D Vision
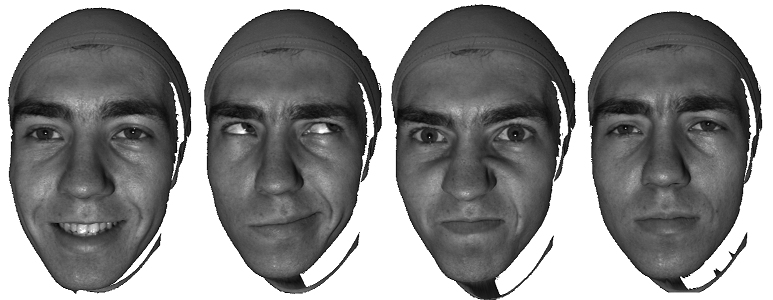
3D scanning and digital geometry processing play fundamental roles in the Metaverse. The 3D scanning lab is developing cutting 3D camera systems,
which combines light field camera calibration, multiwave length phase shifting structured light to capture point clouds, then
use Lie-algebraic cohomology for point cloud fusion and Poisson reconstruction. The system is capable of capturing high resolution
and high speed human facial surfaces with dynamic expressions.
The geometric surfaces are processed with algorithms based on conformal geometry
and optimal transportation, including parameterization, remeshing, registration, comparison and so on.
The Ricci flow method and the optimal transportation map based on geometric variational method are directly applied.
Computational Conformal Geometry
Conformal Structure is a natural geometric structure on surfaces, which governs many physics phenomena,
such as heat diffusion, electric-magnetic fields, etc. Conformal field theory plays fundamental role in string theory.
In mathematics, conformal means "angle preserving". Conformal structure is a specail atlas of the surface, such that angles among tangent
vectors can be coherently defined on different local coordinate systems. Furthermore, concepts in complex anylasis can be
defined on the surface via conformal structure. Conformal geometry is the intersection of algebraic geometry, differential
geometry, complex anylasis and algebraic topology.
In engineering, conformal structure is between topological structure and geometric structure, which is more rigid than topology and
more flexible than geometry. Therefore, conformal structure leads to canonical non-rigid deformation, which is
important for engineering applications, especially for shape anylasis, classification and registration.
The goal of computational conformal geometry is to convert
concepts and theorems from Riemann surface theory to practical algorithms, and implement them
for engineering applications.
Riemann Surface and Holomorphic Differentials
A surface with a conformal structure is called a Riemann surface. All metric surfaces are Riemann surfaces. The image illustrates the conformal structure using isothermal coordinates. The algorithm is based on computing
holomorphic differentials on Riemann surfaces.
Uniformization and Ricci Flow
Surface uniformization means that all metric surfaces can be conformally mapped to one of the three canonical domains, the sphere, the plane and the hyperbolic space. The figures show the uniformization for surfaces with various topologies. Unformization converts general 3D geometric problems to 2D problems in these canonical domains.
Ricci flow is a powerful geometric analytic tool, which has been applied to prove Poincare conjecture.
Ricci flow is a parabolic system of partial differential equations which acts like
the heat equation to spread the curvature of a Riemannian metric evenly over the surface to produce a metric of constant curvature.
Computational discrete Ricci flow is the practical method to compute surface uniformization, it has many important applications in many engineering fields.
Algorithms
Algorithms for computing conformal mappings from a surface onto the canonical domain can be summarized as follows:
-
Genus zero closed surface, the conformal mapping can be commputed using
Spherical Harmonic Maps
.
- Genus zero surface with multiple boundary components, the conformal mapping can be computed using Generalized Koebe's Method, or slit map method.
- Genus one surface, the conformal mapping can be commputed using holomorphic one forms. Another algorithm is to use Euclidean Ricci flow.
-
Higher genus surfaces, the mapping can be commputed using
Hyperbolic Ricci Flow.
- Quasiconformal mappings can be computed using Auxiliary Metric Method.
Applications
Applications of computational conformal geometry in engineering fields are innumerous. It offers the rigorous theoretic frame work for computing surface matching, registration, classification and analysis. The followings are a few examples in the most directly related fields:
Monograph Books
The followings are books summarizing my research:
- Classical and Discrete Differential Geometry
- Computational Conformal Geometry
- Variational Principles for Discrete Surfaces
-
Ricci Flow for Shape Analysis and Surface Registration
-
Conformal Geometry, Computational Algorithms and Engineering Applications
- Computational Conformal Geometry Theory
- Optimal Transportation Theory and Computation
More information about the books can be found through the online links.